Чему равна сумма целых натуральных чисел от 1 до бесконечности? Безусловно бесконечности, чему же еще. Однако видео по вот этой ссылке http://www.youtube.com/watch?v=E-d9mgo8FGk доказывает, что сумма натуральных чисел равна -1/12. Минус одна/двенадцатая!
Сопровождающий текст на английском, но математика понятна и доступна ученику начальных классов без перевода. Только сложения, вычитания, никаких сложных действий.
Засада кроется в самом начале. Когда авторы рассматривают последовательность 1-1+1-1+1-….. они утверждают, что там, в бесконечности, в конце концов результат этой последовательности действий будет либо «один» либо «ноль». Однако мы не знаем, где она там закончится, поэтому вывод — результат равен 1/2. Если принять это за основу все дальнейшее становится логичным и сумма всех натуральных чисел действительно равно -1/12.
Не могу притянуть математику, чтобы опровергнуть первый расчет 1/2. Если идти через лимиты, то не совсем понятно, какую функцию подставить. Интегральная оценка действительно должна дать в пределе 1/2. Оптическая — возьмем белый цвет и черный и будем быстро их переключать — тоже даст серый 1/2 🙂 Вероятностная тем более.
По хорошему если описать 1-1+1-1+1-… функцией, то значение функции при числе элементов равное бесконечности должно быть не определено. Соответственно все остальные рассуждения дальше рушатся. Но может быть есть другие варианты? У кого как с математикой?
P.S.: Хорошо дети выросли. Старший подсказывает, что в качестве функции можно рассмотреть (-1) в степени n, при n стремящейся к бесконечности. В конечном итоге если откинуть первые члены, можно оставить (-1) в степени бесконечность. Если подогнать под предел, получается ряд, который не сходится. А раз он не сходится, то и решения нет. Дурят нашего брата.
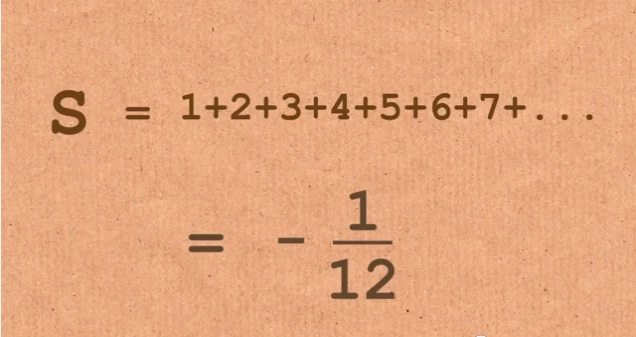
Как то все странно. 🙂
Кажется ведь 1 + 2x + 3x^2 + 4x^3+… = 1/(1-x)^2 верно только если x<1 по модулю. т.е от -1 до 1 не включая сами 1 и -1. А они вместо х подставляют -1. Отсюда и косяк кажется.
не вкурил, перечитаю ещё раз……
Пересмотреть надо, вся тема в ролике.
Пожалуй я даже не соглашусь с предположением, что при частой смене «черного» и «белого» вдруг получим «серый»!? Получить конечно можно, но как аксиому считать не сталбы… Так и в ролике «проффесор» запутывает оператора… в конце концов тот задает ключевой вопрос типа «Как это возможно?» на что проффесор говорит «I dont know!, but…»
Безусловно, математика — царица всех наук, физику я подтянул очень схематически. «Серым» ряд станет в динамике, пока счетчик бежит вдоль него, но не в пределе 🙂
Кстати, -1 брать за основу никак нельзя, т.к. се не есть число натуральное…
а где в расчете -1 брали?
курите тут
http://ru.wikipedia.org/wiki/Ряд_Гранди
Спасибо! Получается ребята вытащили на свет старую тему.
Попробуй применить метод суммирования Чезаро, для 1-1+1-1+1-1…. Для продолжения тебе уже кто-то ряд Гранди посоветовал)
ну как ни крути -1/12 не получишь.
1-1+1-1+1-1+1…=x
Очевидно что x равен либо 1 либо 0. Если ответ 1 то 1-х=0, если ответ 0 то 1-x=1 Проверим.
1-(1-1+1-1+1-1+1…)=…откроем скобочки…=1-1+1-1+1-1+1…
то есть
1-(1-1+1-1+1-1+1…)=1-1+1-1+1-1+1…
то есть
1-x=x
значит
1=x+x
1=2x
1/2=x
1-1+1-1+1-1+1…=1/2
Это наверное самый простой способ объяснить, но есть более сложные и куда более убедительные..
А -1/12 это низший энергетический уровень бозонной струны в квантовой физике, так что эта величина есть и в природе. Просто нам с нашим линейным мышлением сие кажется странным. Вот и не верится.
В принципе ваш тоже вполне убедителен!
Интересный момент. Вопрос только в случайном совпадении или не познанной закономерности? Если закономерность познана, то насколько она верна при определенной спорности теории струн в свете более поздних теорий?
Х не может равняться 1/2, так уравнение 1-х=1 будет неверно.
То, что Вы написали, а Вы написали 1-x=1, находится под одним из двух условий «Если».
А там пришли в итоге ни к тому и ни к тому, а промежуточному варианту:
1-x=x.