Учи математику — не будь идиотом!

Одной из непосильных для меня задач является попытка объяснить детям, для чего нужно учиться. То есть общее понимание есть как бы у всех, хорошо учишься в школе, значит поступаешь в хороший институт, получаешь хорошую профессию, находишь хорошую работу. По-крайней мере шансы велики. А вот для чего в реальной жизни нужны синусы, пифагоры, моменты и прочая «лабудистика» сразу и не ответишь. Поэтому мотивация пропадает. Можно придумывать искусственные примеры, но детям сразу видно, что они надуманы.

Недавно мне подвернулся очень удачный шанс. Причем, и как нельзя кстати, оказалось и само название этого «шанса» — не будь идиотом.

Сейчас у всех популярны различные мотиваторы/демотиваторы и вот младший ребенок, зная мое трепетное отношение к математике, приносит мне iPhone, на экране которого очередной демотиватор:

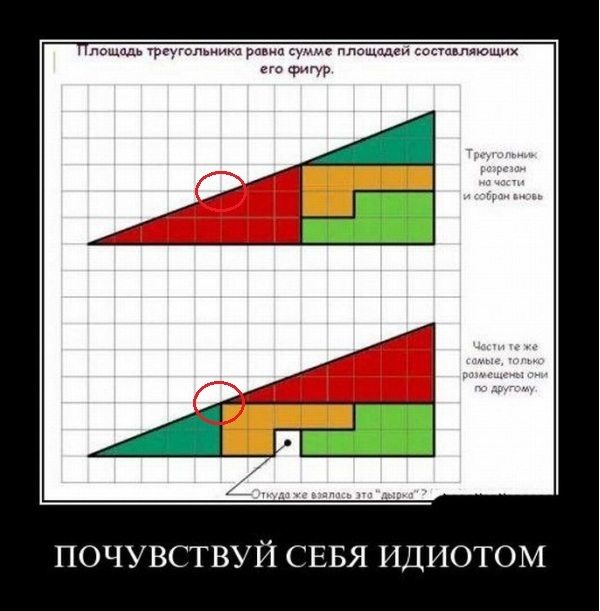
Вопрос простой — куда делся квадратик. Высота и длина треугольников осталась одной и той же. Легко почувствовать себя идиотом. Но только не в том случае, если у вас есть вера.

У меня она есть, я верю в математику, не зря ее называют единственной точной наукой. И царицей всех наук.

— Игорь, — начал я очередное нравоучение, — математика, самая точная наука. 2+2 всегда 4. Если тебе показывают, что это не так, не верь своим глазам, не верь ушам, даже мозгу не верь. Верить можно только математике. Давай разбираться. Так как уши, нос и осязание здесь незадействованы, значит обманывают твои глаза и/или мозг. Возьми, нарисуй на бумаге эти фигурки и проверь.

Черз полчаса мне принесли 4 обгрызка из тетради в клеточку, на которых убедительно доказалось, что математика все-таки бывает и дает сбои.  Пришлось засучивать рукава. И передоказать, что это не математика сбоит, а физика.

Открываем excel, форматируем размеры столбов и строк, чтобы они были квадратными и рисуем крупно тот же самый треугольник. Потом делаем копию, перемешиваем и получаем новый вариант. Опссс. Квадратик пустой. Ребенок довольный.

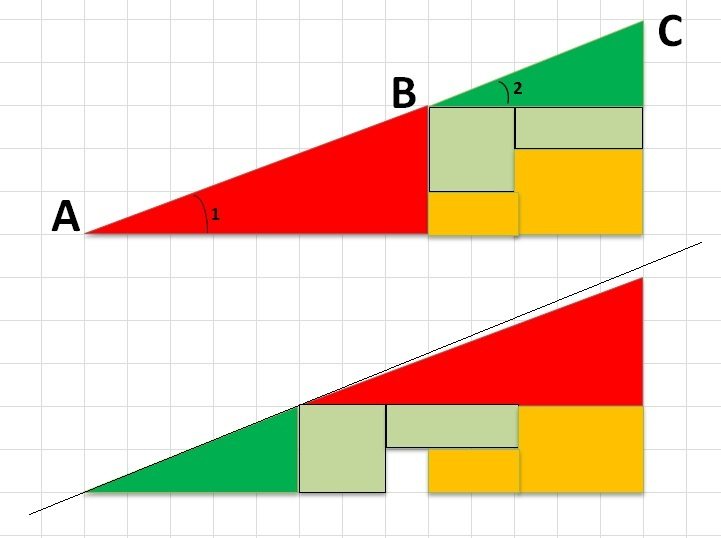
Но я еще не закончил. Накладываю один рисунок на другой.

— Так ты криво треугольник нарисовал, — вдруг замечает Игорь. Правильно, гипотенуза АС треугольника при ближайшем рассмотрении — это не прямая линия. И между первым и вторым треугольником в точке В  наблюдается небольшое расхождение.  (посмотрите внимательно по линиям клеток). А примечание возле рисунка с демотиватором откровенно вводит в заблуждение —  якобы разрезан на части целый треугольник.
— Вот из-за этого расхождения и набегает пустой квадратик — подвожу итог.
— Не может быть! Чтобы из-за вот этой маленькой полосочки? Ты просто неправильно нарисовал, у тебя красный и зеленый треугольники с разными углами получились, а должны быть одинаковыми.

— Т.е. ты считаешь, что  углы должны быть одинаковыми и гипотенуза АС — прямой?
— Получается что так, — на всякий случай с сомнением произнес Игорь
— Отлично, тогда начинаем считать. Вначале давай вычислим какой будет гипотенуза у красного и у зеленого квадрата, это просто:

гипотенуза = корень (8*8+3*3) ….

Смотря на мои манипуляции Игорь вдруг радостно закивал
— Это же теорема Пифагора, да?!!!
— Конечно да! Итак, гипотенузы расчитали. Теперь давай определим, чему равны углы.
— А это как?
— А что вы проходили перед новым годом, всего 2 недели назад?
— Синусы и косинусы…
— Вот и находим синус. Делим катет на гипотенузу, далее по результату определяем с помощью арксинуса угол, ексель нам в помощь. У зеленого он равен около 20 градусов,  у красного чуть больше  21 градуса.  Т.е. в 1-м случае гипотенуза АС вогнута вниз, а во втором выгнута вверх, и за счет этой разницы набегает целый квадрат.

Еще раз внимательно смотрим на картинку с демотиватора при хорошем увеличении. Разница заметна и на ней.

Но чтобы окончательно закрепить результат, делаю еще один шаг.
— давай посмотрим эту же картинку, но только уменьшим размеры треугольников. Уже видно, что оптический обман достигается за счет увеличения длины «гипотенузы». И чем она больше, тем меньше видно разницу. А если сделать ее короткой?

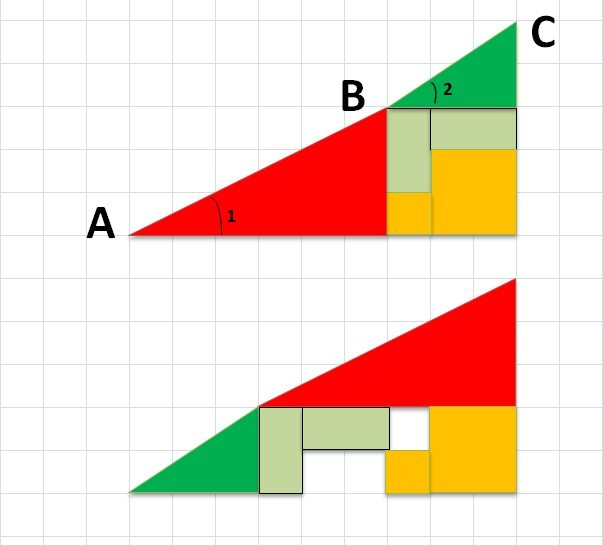
Вот вам и окончательный результат. Оказывается «бесследно» исчезает уже не один квадратик, а целых три. Зато в этом варианте отлично видно, куда именно они исчезают.

А если бы углы были одинаковыми, т.е. мы действительно разрезали целый треугольник? Тогда получилась бы следующая картинка:

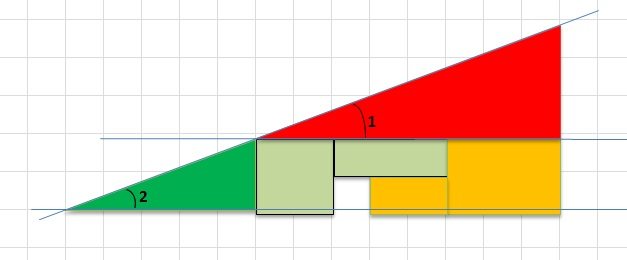
После этого показал Игорю на его полку с книгами, на которой уже покрылась пылью и «Занимательная математика», и «Занимательная физика», и другие замечательные и занимательные книжки. Рассказывающие о таких фокусах, после которых исчезнувший квадрат покажется детской шалостью.

Кстати, когда уже была готова статья и осталась только нажать на кнопку «опубликовать» вдруг увидел ошибку. Не очень критичную, скорее даже нелепую. Вот думаю, опозорился бы 🙂 Поэтому на всякий случай перепроверьте, а то  всякое бывает …..